Generate a random number which is relatively prime with (p-1) and (q-1). Let the number be called as e. Calculate the modular inverse of e. The calculated inverse will be called as d. Algorithms for generating RSA keys. We need two primary algorithms for generating RSA keys using Python − Cryptomath module and Rabin Miller module. The short answer is: each time you need to access your RSA private key, your password is used as a 'seed' to re-generate the AES-256 key that you need to decrypt your RSA private key (keep reading for details). RSA Key Generation. When generating an RSA key, you want it as random as possible, pulling randomness from the operating system's.
- Cryptography with Python Tutorial
- Useful Resources
- Selected Reading

In this chapter, we will focus on step wise implementation of RSA algorithm using Python.
Generating RSA keys
The following steps are involved in generating RSA keys −
Create two large prime numbers namely p and q. The product of these numbers will be called n, where n= p*q
Generate a random number which is relatively prime with (p-1) and (q-1). Let the number be called as e.
Calculate the modular inverse of e. The calculated inverse will be called as d.
Algorithms for generating RSA keys
We need two primary algorithms for generating RSA keys using Python − Cryptomath module and Rabin Miller module.
Cryptomath Module
The source code of cryptomath module which follows all the basic implementation of RSA algorithm is as follows −
RabinMiller Module
The source code of RabinMiller module which follows all the basic implementation of RSA algorithm is as follows −
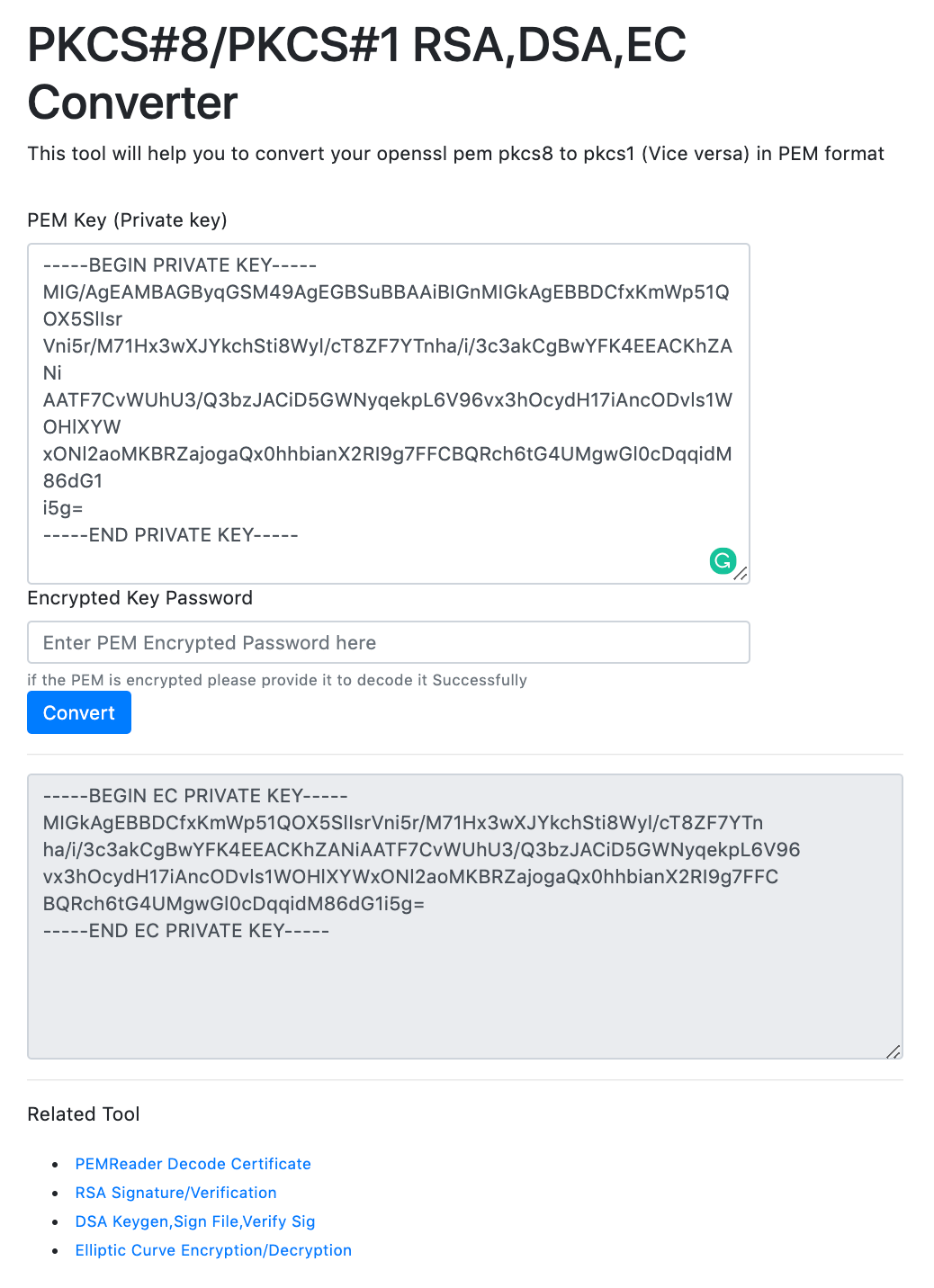
The complete code for generating RSA keys is as follows −
Output
The public key and private keys are generated and saved in the respective files as shown in the following output.
In order to be able to create a digital signature, you need a private key. (Its corresponding public key will be needed in order to verify the authenticity of the signature.)
In some cases the key pair (private key and corresponding public key) are already available in files. In that case the program can import and use the private key for signing, as shown in Weaknesses and Alternatives.
In other cases the program needs to generate the key pair. A key pair is generated by using the KeyPairGenerator class.
In this example you will generate a public/private key pair for the Digital Signature Algorithm (DSA). You will generate keys with a 1024-bit length.
Generating a key pair requires several steps:
Create a Key Pair Generator
The first step is to get a key-pair generator object for generating keys for the DSA signature algorithm.
As with all engine classes, the way to get a KeyPairGenerator object for a particular type of algorithm is to call the getInstance static factory method on the KeyPairGenerator class. This method has two forms, both of which hava a String algorithm first argument; one form also has a String provider second argument.
A caller may thus optionally specify the name of a provider, which will guarantee that the implementation of the algorithm requested is from the named provider. The sample code of this lesson always specifies the default SUN provider built into the JDK.
Put the following statement after the
line in the file created in the previous step, Prepare Initial Program Structure:
Initialize the Key Pair Generator
Generate Rsa Key Pair
The next step is to initialize the key pair generator. All key pair generators share the concepts of a keysize and a source of randomness. The KeyPairGenerator class has an initialize method that takes these two types of arguments.
Openssl Generate Rsa Private Key
The keysize for a DSA key generator is the key length (in bits), which you will set to 1024.
The source of randomness must be an instance of the SecureRandom class that provides a cryptographically strong random number generator (RNG). For more information about SecureRandom, see the SecureRandom API Specification and the Java Cryptography Architecture Reference Guide .
The following example requests an instance of SecureRandom that uses the SHA1PRNG algorithm, as provided by the built-in SUN provider. The example then passes this SecureRandom instance to the key-pair generator initialization method.
Generate Rsa Private Key Windows
Some situations require strong random values, such as when creating high-value and long-lived secrets like RSA public and private keys. To help guide applications in selecting a suitable strong SecureRandom implementation, starting from JDK 8 Java distributions include a list of known strong SecureRandom implementations in the securerandom.strongAlgorithms property of the java.security.Security class. When you are creating such data, you should consider using SecureRandom.getInstanceStrong(), as it obtains an instance of the known strong algorithms.
Generate Private And Public Key
Generate the Pair of Keys
The final step is to generate the key pair and to store the keys in PrivateKey and PublicKey objects.